De stijgende lijn van onze puzzelsnelheid

Gepubliceerd op: 14 Nov 2025
De afgelopen jaren hebben we tientallen puzzelsessies vastgelegd om beter te begrijpen hoe onze puzzelsnelheid zich ontwikkelt. Daarbij rees één belangrijke vraag: worden we als duo eigenlijk wel sneller? Of lijkt dat vooral zo doordat we sommige puzzels vaker leggen en profiteren van herkenning? In dit artikel onderzoeken we die vraag aan de hand van onze eigen puzzeldata. Door de dataset te filteren, te normaliseren en door de tijd heen te analyseren, ontstaat een helder beeld van onze echte voortgang als speedpuzzelaars.
Dataset analyse
Voor dit onderzoek heb ik mijn volledige puzzelgeschiedenis als uitgangspunt genomen. Die dataset bevat alle 467 tijden die ik de afgelopen jaren heb geregistreerd. Niet elke sessie is echter geschikt om puzzelsnelheid eerlijk te analyseren. Daarom pas ik meerdere selectiecriteria toe om tot een consistente, betrouwbare en vergelijkbare dataset te komen.
Om te laten zien hoe de dataset wordt teruggebracht tot een logisch geheel, heb ik drie visuele verdelingen gemaakt: het aantal stukjes, het puzzelmerk en de groepsgrootte. Deze grafieken tonen de verhoudingen binnen de volledige dataset en laten zien waarom de uiteindelijke dataset logisch en goed onderbouwd is.

Filteren op 1000 stukjes en Jan van Haasteren puzzels
Om puzzelsnelheid eerlijk te kunnen analyseren, is het belangrijk om uitsluitend 1000-stukjes puzzels mee te nemen. Dit formaat komt het meest voor in mijn dataset en voorkomt dat verschillen in stukgrootte of opbouw de analyse vertekenen.
Daarnaast delen Jan van Haasteren-puzzels een herkenbare stijl en structuur. Door alleen deze puzzels te gebruiken, blijft de dataset inhoudelijk consistent en vergelijkbaar, zonder variatie in merk of ontwerp die tot scheve conclusies zou kunnen leiden.
Waarom alleen duo-sessies zijn meegenomen
Duo-sessies vormen de basis van mijn puzzeldata en leveren de meest stabiele inzichten op. Grotere teams leggen puzzels sneller door taakverdeling en solo-sessies zijn van een totaal andere dynamiek. Door alleen duo-pogingen te gebruiken, blijft de vergelijking eerlijk en consistent.
Duo-sessies vormen daarentegen een stabiele en consistente puzzelvorm. De manier van samenwerken blijft door de jaren heen vrijwel gelijk, en de dynamiek is eenvoudiger te modelleren dan die van grotere teams. Omdat duo’s bovendien de grootste groep vormen binnen de gefilterde dataset, zijn ze de meest logische en betrouwbare basis voor deze analyse.
Overgebleven datapunten na filtering
Na alle filters blijft een dataset over van 116 registraties, wat neerkomt op ongeveer 22% van de oorspronkelijke dataset. Dit vormt een compacte maar betrouwbare basis om trends door de jaren heen te analyseren.
Puzzelsnelheid
Om puzzels met elkaar te kunnen vergelijken, is een eenduidige maat voor snelheid nodig. In deze analyse wordt puzzelsnelheid uitgedrukt in stukjes per minuut. Dat maakt het mogelijk om puzzeltijden eerlijk te vergelijken, ongeacht of een puzzel 90 minuten of 120 minuten heeft geduurd.
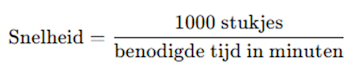
Een puzzel die in 100 minuten wordt gelegd heeft dus een snelheid van 10 stukjes per minuut. Een puzzel die in 80 minuten wordt gelegd, komt uit op 12,5 stukjes per minuut. Deze snelheid vormt de basis voor de grafieken die de ontwikkeling door de jaren heen laten zien.
Gemiddelde puzzelsnelheid per maand
De maandelijkse ontwikkeling van onze puzzeltijden geeft een goed beeld van hoe onze prestaties zich door de jaren heen hebben ontwikkeld. In onderstaande grafiek is voor elke maand het gemiddelde genomen van alle beschikbare duo-sessies met 1000-stukjes Jan van Haasteren-puzzels.
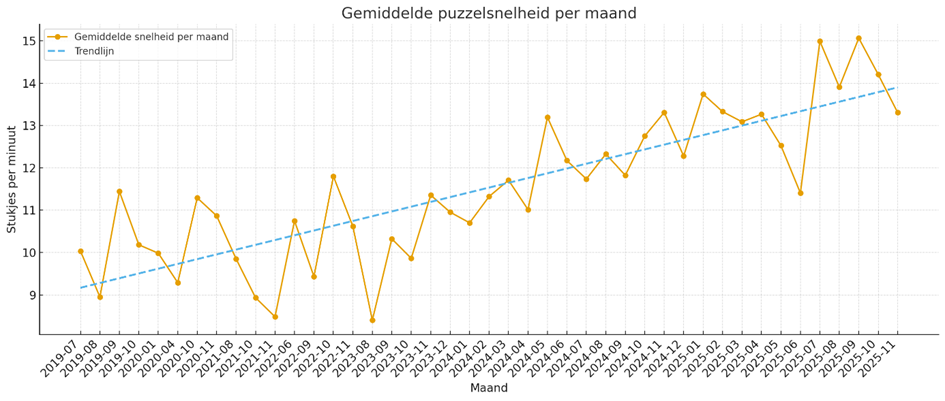
Hoewel de maandelijkse waarden duidelijk schommelen laat de trendlijn een duidelijke stijging zien. Door de jaren heen leggen we dezelfde soort puzzels steeds sneller, en dat patroon is ook zonder verdere analyse al helder zichtbaar.
Herhalingen
We merken zelf dat we sommige puzzels graag opnieuw leggen. Dat zie je ook duidelijk terug in de data: een deel van de puzzels komt maar één keer voor, maar veel puzzels leggen we twee of drie keer, en een paar zelfs nog veel vaker. In de grafiek hieronder zie je hoe vaak onze puzzels zijn herhaald. De grootste groep bestaat uit puzzels die één of twee keer zijn gelegd, gevolgd door enkele echte favorieten die we drie keer of vaker hebben gemaakt.
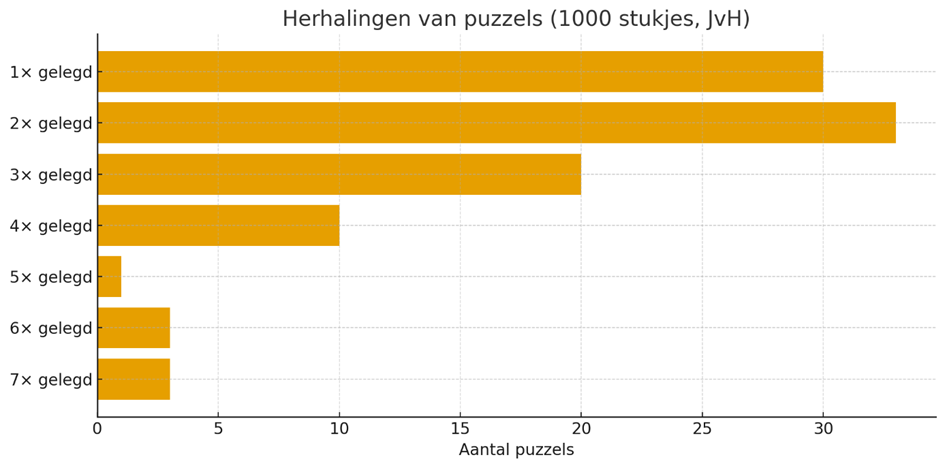
Normalisatie op basis van herhaling
Omdat veel puzzels in onze dataset meerdere keren zijn gelegd, levert elke extra poging een snelheidsvoordeel op. Bij een tweede of derde keer leggen we dezelfde puzzel bijna altijd sneller, vooral door herkenning van kleuren, patronen en lastige zones. Dat herhalingseffect is interessant op zichzelf, maar vertroebelt het beeld als we willen weten of we als speedpuzzelaars echt beter worden.
Daarom berekenen we eerst voor alle puzzels samen een algemene herhaalfactor per poging. Voor elke poging 𝑖 vergelijken we de snelheid van die poging met de eerste keer dat die puzzel is gelegd:

Dit wordt gedaan voor alle puzzels waarvoor poging 𝑖 bestaat.
Uit deze analyse blijkt onder andere dat tweede pogingen gemiddeld duidelijk sneller zijn dan eerste pogingen, derde pogingen nog wat sneller, en vierde (of latere) pogingen nog meer voordeel opleveren. Dit is de snelheidsverhoging die je krijgt puur door herkenning.
Om puzzelsessies eerlijk met elkaar te kunnen vergelijken, corrigeren we vervolgens iedere poging met de bijbehorende herhaalfactor:

Hiermee rekenen we elke sessie terug naar een snelheid alsof het de eerste keer was dat die puzzel gelegd werd. Herhalingseffect wordt zo uit de data gehaald, terwijl verschillen tussen jaren juist zichtbaar blijven.
De grafiek hieronder laat zien hoeveel sneller we een puzzel leggen wanneer we deze vaker maken. Bij de tweede poging ligt onze snelheid gemiddeld al zo’n 12% hoger dan bij de eerste keer, en dat voordeel loopt verder op bij poging drie, vier en vijf. Vanaf de zesde keer ontstaat een plateau: extra herhaling levert dan nog maar beperkt winst op. Dit herhaalvoordeel ontstaat volledig door herkenning en is dus belangrijk om weg te filteren wanneer we willen bepalen of we als speedpuzzelaars écht beter worden.
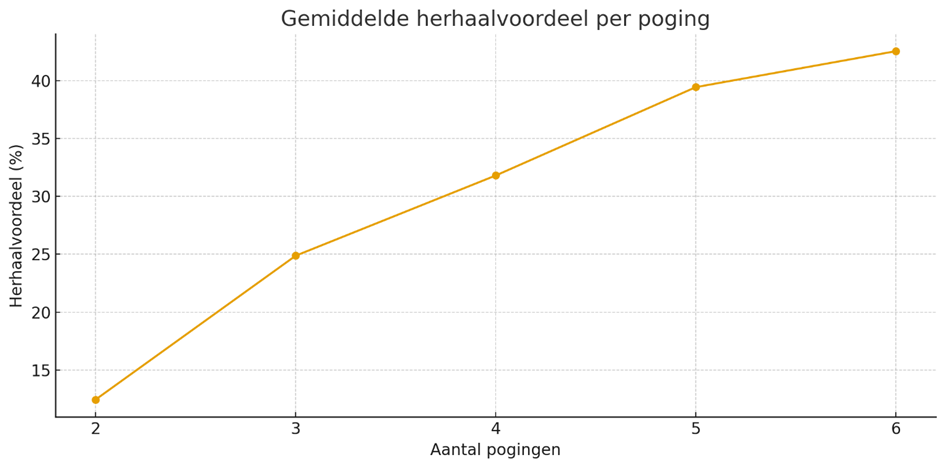
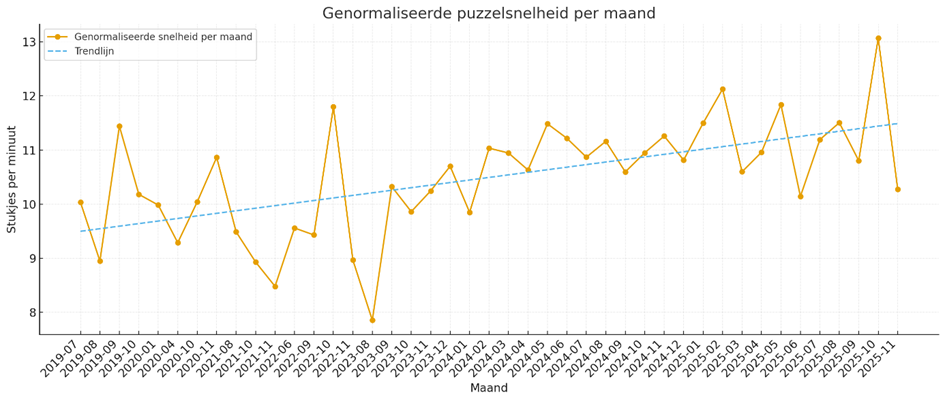
Gemiddelde puzzelsnelheid per maand genormaliseerd
De grafiek hieronder laat zien hoe onze puzzelsnelheid zich ontwikkelt wanneer het herhaalvoordeel volledig wordt verwijderd. Door elke poging terug te rekenen naar het niveau van een eerste poging, blijft alleen onze echte puzzelvaardigheid over. Zelfs zonder herhalingswinst blijft een duidelijke stijgende lijn zichtbaar. Nieuwe puzzels leggen we tegenwoordig sneller dan in eerdere jaren, waarbij recente maanden waarden rond de 11 tot 12 stukjes per minuut laten zien.
Voorbeelden uit de dataset
Om onze vooruitgang als speedpuzzelaars inzichtelijk te maken, lichten we twee puzzels uit die elk op een andere manier laten zien hoe onze puzzelvaardigheid zich heeft ontwikkeld.
Rondje Texel — een uitzonderlijk snelle eerste poging
In oktober 2025 legden we Rondje Texel voor het eerst. Zonder enige vorm van herkenning haalden we direct een snelheid van ruim 15 stukjes per minuut. Zulke snelheden zagen we in eerdere jaren vrijwel alleen bij herhaalde pogingen. Dit maakt deze puzzel een duidelijk voorbeeld van hoe sterk onze basisvaardigheid inmiddels is: we kunnen nieuwe puzzels tegenwoordig op een tempo leggen dat vroeger alleen bij “ingeoefende” puzzels voorkwam.
Kamperen in het Bos — sterke progressie door herhaling
De puzzel Kamperen in het Bos laat vooral zien hoe we door herhaling steeds beter worden. Bij de eerste poging lagen we rond de 10,9 stukjes per minuut, maar bij de zesde poging steeg dat tempo naar ruim 16,5 stukjes per minuut. Dit is een groei van bijna 6 stukjes per minuut. Een deel hiervan komt uiteraard door herkenning, maar de omvang van de verbetering laat zien dat ook onze aanpak, samenwerking en bouwvolgorde steeds efficiënter zijn geworden.
Conclusie
Uit de volledige analyse blijkt duidelijk dat onze puzzelsnelheid de afgelopen jaren merkbaar is toegenomen. Ook wanneer het herhaalvoordeel volledig wordt weggehaald, laat de genormaliseerde trendlijn zien dat onze basisvaardigheid blijft stijgen. Nieuwe puzzels leggen we tegenwoordig op een tempo dat we in eerdere jaren niet haalden, en bij herhaalde puzzels worden we niet alleen sneller door herkenning, maar ook efficiënter in aanpak en samenwerking.